Data Structures

“In computer science, a data structure is a data organization, management, and storage format that enables efficient access and modification.” - https://en.wikipedia.org/wiki/Data_structure

Why care?

Suitable data structures affect the performance of your application. You can increase quality and performance by choosing the right data structure and accomanying algorithm. This feels like something we should care about.

Additionally Big O Notation is worth understanding as this is how the complexity is rated.

Array

Complexity: O(1) Constant time / complexity to access data. Searching, Inserting, Deleteing is O(n) Linear time / complexity
Use case: Fixed size collection that dont change, can store all types of data. Smaller tasks where you wont be interacting with the data that often

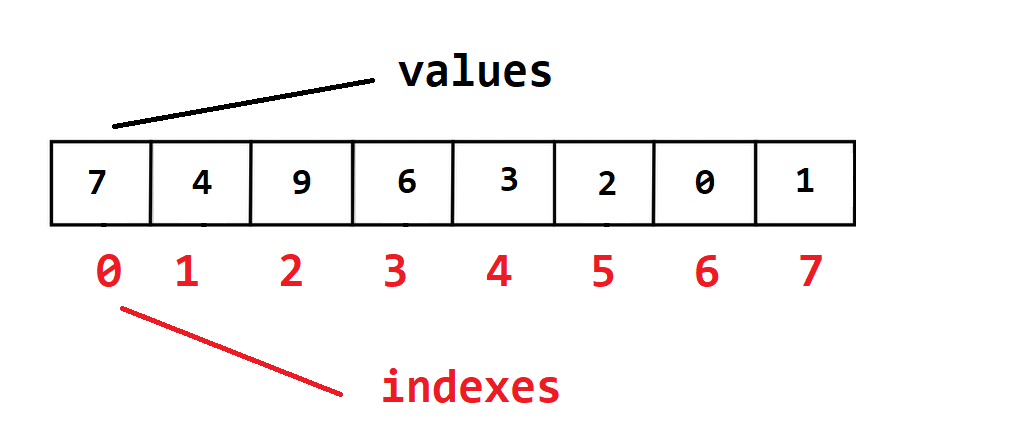
arrays (linear data structure, all of the same type)

An array is a linear data structure that collects elements of the same data type and stores them in a sequential manner one after the other. This is a Random Access data structure.

1
int[] array = new int[42];

References

ArrayList

Complexity: O(1) Constant time / complexity to access data. Searching, Inserting, Deleteing is O(n) Linear time / complexity
Use case: Dynamic size, can only store object (so no primative types although they are auto boxed for you). More interactive programs where you’ll be modifying data often

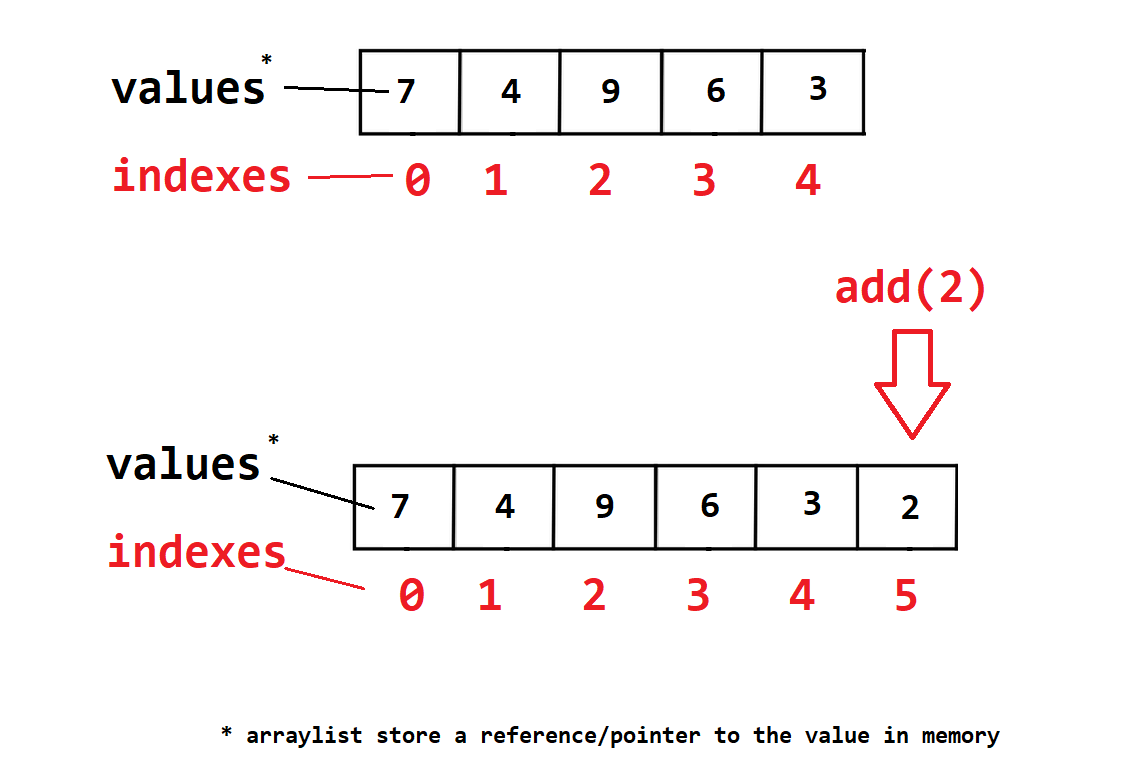
arraylist)

Fundametially this is a growing array, this means an ArrayList is dynamic and expands as needs. Its backed by an array in memory, this is managed by the ArrayList class.

The ArrayList stores references/pointers to the locations of its objects in memory, this is why it can grow in size. This means the data is not stored contiguously (as consecutive blocks of memory).

From the class it will inherit pre-built methods that we can use, there are a few which not all langauges implement. The most common are which you could find are

  • Add
    • Add(Object) will append to the end of the array list where no value exists. If you pass a primative type like Add(2) it will convert the 2 to an Integer(2) object which is auto boxing
    • Add(Object, index) will add the element you pass at the given index. If the index is taken it will shift the values over to the next avalible index
  • Remove
    • Remove(index) will remove the element at that index location
    • Remove(Object) will remove the first instance of that Object in the array list
    • Both return -1 if nothing is found to be removed
    • The size of the array list doesnt change
  • Get
    • Get(index) will return the value at that location
  • Set
    • Set(index, Object) is used to replace elements in the array list, it will set element at the index which you passe in to the object you also passed in
  • Clear
    • Clear everything in the array list, the size doesnt change
  • toArray
    • var newArray = arrayList.toArray() will convert an array list to an array, the array will be an array of objects
1
var arrayList = new ArrayList(); // auto array size will be 10

References

Binary Search Tree

Complexity: O(log n) Logarithmic time / complexity
Use case: Insert, find and delete

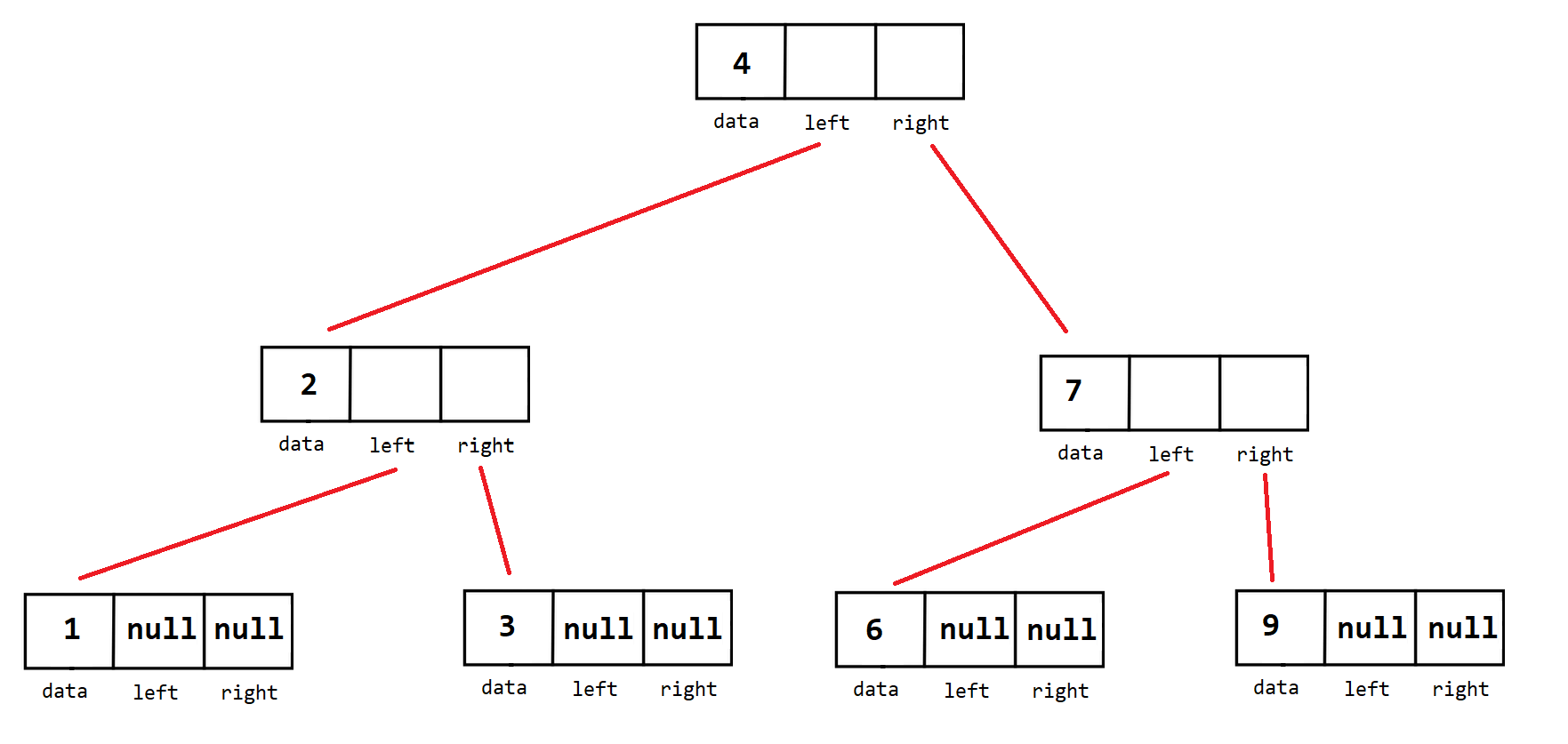
binary-search-tree

Supports Binary Search Algorithm to find a targeted value in a sorted array. A tree is a collection of nodes with edges that connect them.

  • None-linear, meaning they have a Left and a Right pointer
  • 2 Children Max
    • Child to the left has a value less than or equal to itself
    • Child on the right has a value greater than or equal to itself
  • No 2 nodes can contain the same value
  • Each pass cuts the data in half

References

Dictionary

Complexity: O(1) Constant time / complexity (for insert, find and delete). This is because the hash function will tell us exactly where that key/value is stored
Use case: Insert, find and delete

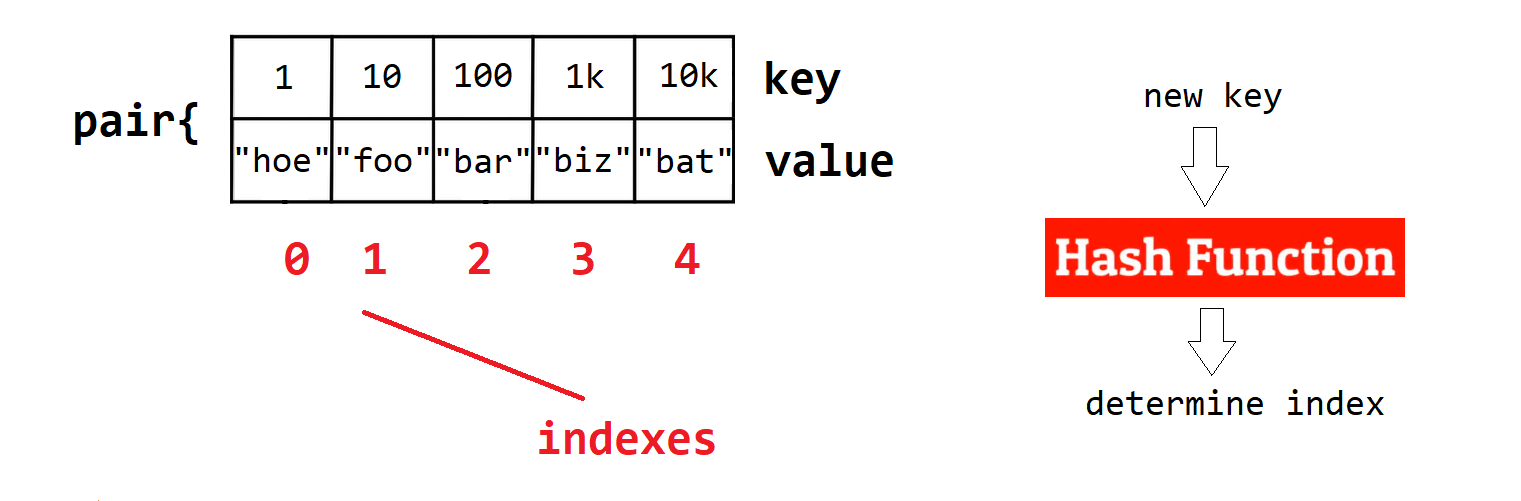
dictionary index is determined by a hash of the key

A Dictionary is an abstract data structure which stores data in the form of key/value pairs, each value has a key associated with it and together they create a pair which is stored in the dictionary data structure as an element of that dictionary. They are also known as maps or associative arrays in some langauges, there is no functional difference and all work in almost identical ways.

The most common way to implement a dictionary is using a hash table/function. By giving a hash function both a key and a table to map it to, it can determine what index location to store that key at in the array. Dictionaries are built upon these Hash Tables and the key’s in our key/value pairs are stored in memory IN these hash tables at indexes which are determined by a hash function.

key: Dictionaries are indexed using the key as opposed to a numerical index like an array. The key’s in a key/value pair can be pretty much any primitive data type, examples int, string, double ect. Keys can only appear once in the dictionary, they have to be unique. Additionally each key can only have 1 value.

value: The pairs can be anything, its very flexible in terms of the combinations of key/values. Examples string, bool or even another dictionary. Duplicate values are allowed as long as the key is unique.

References

Hash sets / Hashtable

  • Hash tables are a way to store information so that we’re able to cut down the amount of nil values while also allowing for the information to be stored in a way that is easily accessible.
  • A hash function will take all the keys for a given dictionary and strategically map them to a certain index location in an array so that it can eventually be retreived easily.
  • Hash collisions
    • are when a hash function takes two keys, example Steven and Sean, hashes them and returns the same index. Example 9
    • this can be resolved using either open addressing or closed addressing
      • open addressing will put the key in some other index location separate from the one returned to us by the hash function. Normally by looking for the next nil value in the table, this is the closest location that has no key already.
      • closed addressing uses linked lists to chain together keys which result in the same hash value

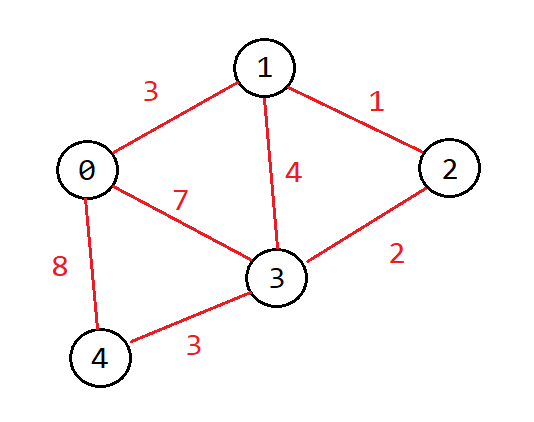
Graph

Complexity: O(V+E) where V is number of vertices in the graph and E is number of edges in the graph.
Use case: Maps, follower system of a majority of social media websites, IP routing and can be used in telephone networks

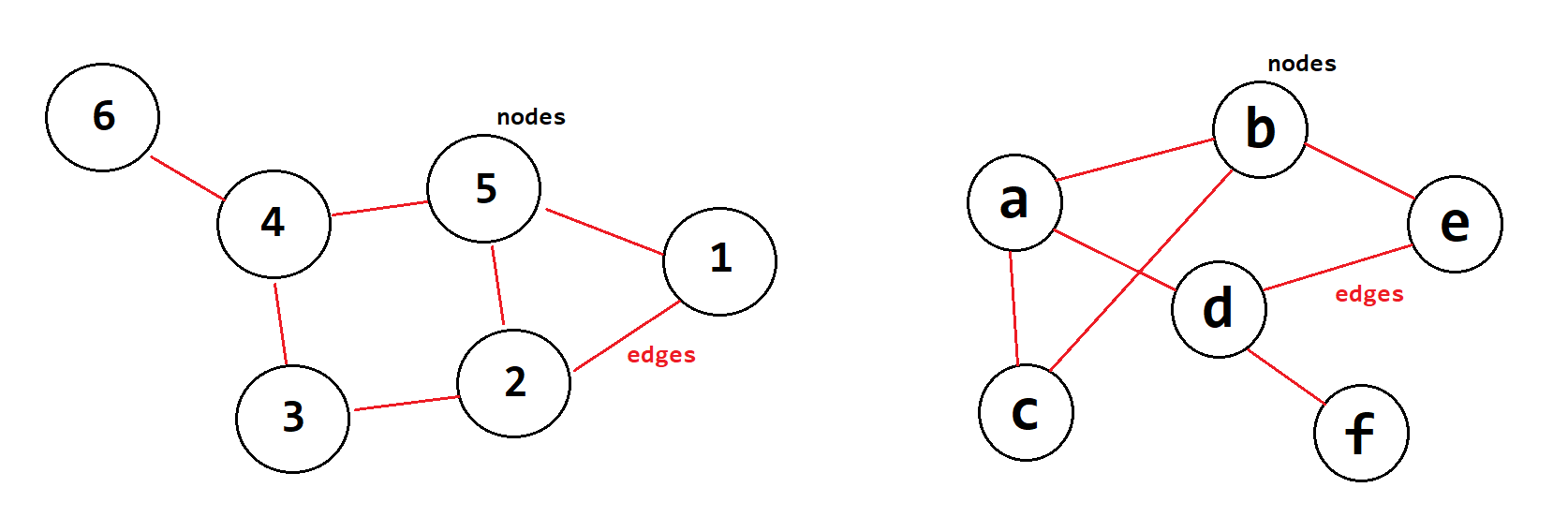
graph: visual representation

The notational representation of a graph is not as easy to understand, this is the above left graph.

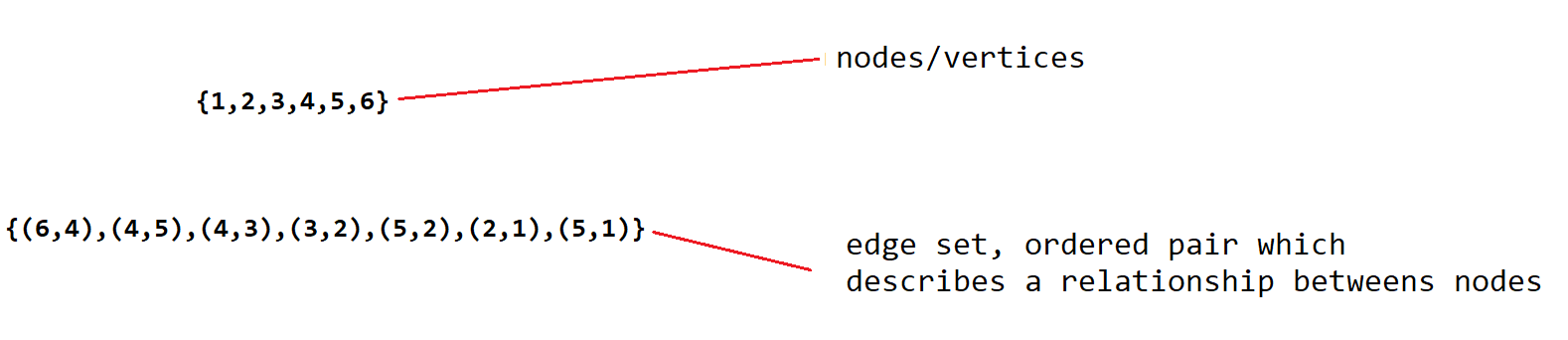
graph: notational representation

Graphs are composed of pieces of information and the paths that run between them. They are a nonlinear data structure consisting of nodes (the information) and edges (the paths that run between them). There are a finite set of nodes (aka vertices). Nodes are connected by the edges.

Graphs have multiple starting points, we can start from any node and traverse to any node that has an edge connecting them.

Properties

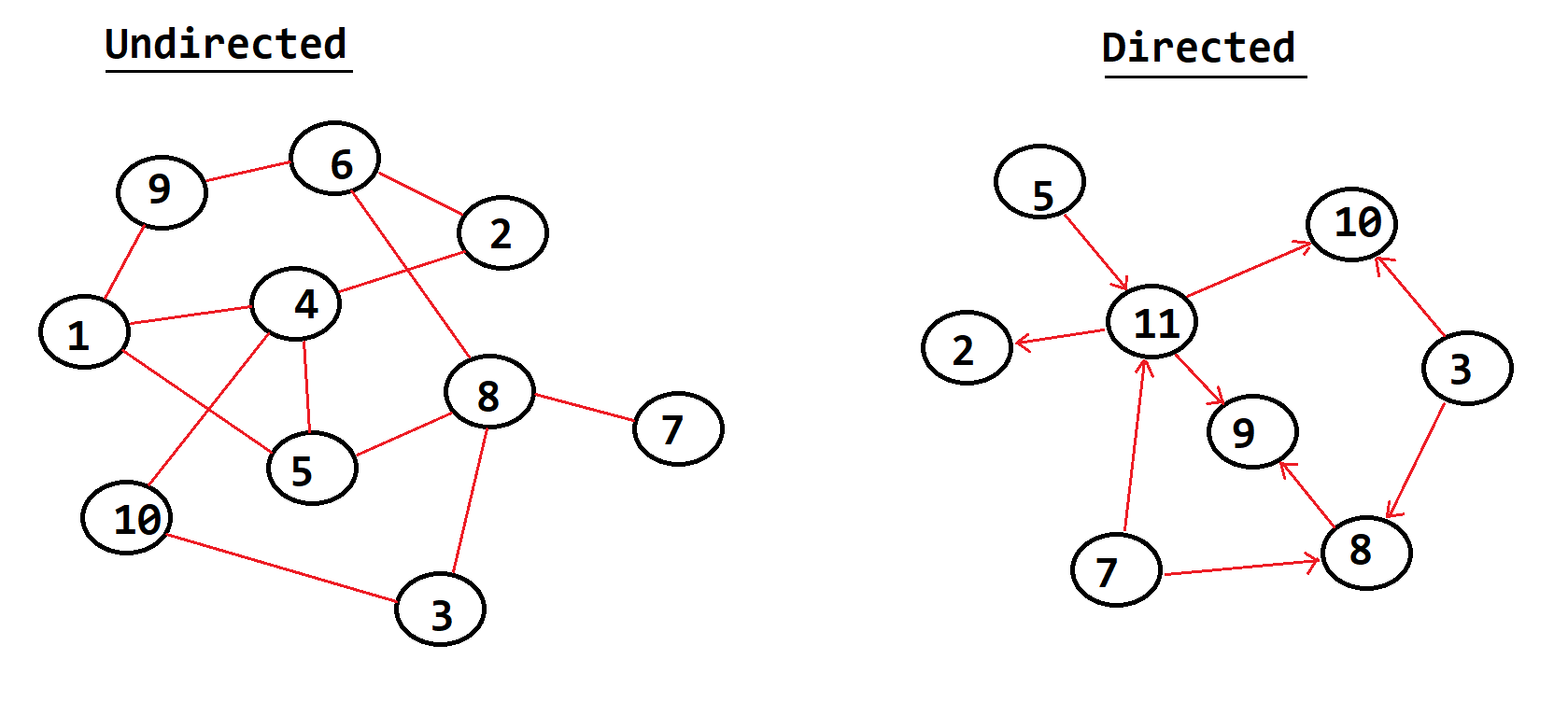
Directed & Undirected

Directed

  • A graph in which the direction you traverse the nodes is NOT important
  • Usually indicated by a lack of arrows
  • We can hop between nodes or even back and forth between them without problems

Undirected

  • A graph in which the direction you traverse the nodes IS important
  • Usually indicated by arrows representing direction, note the edges COULD point both ways but they dont have to

graph: properties directed and undirected

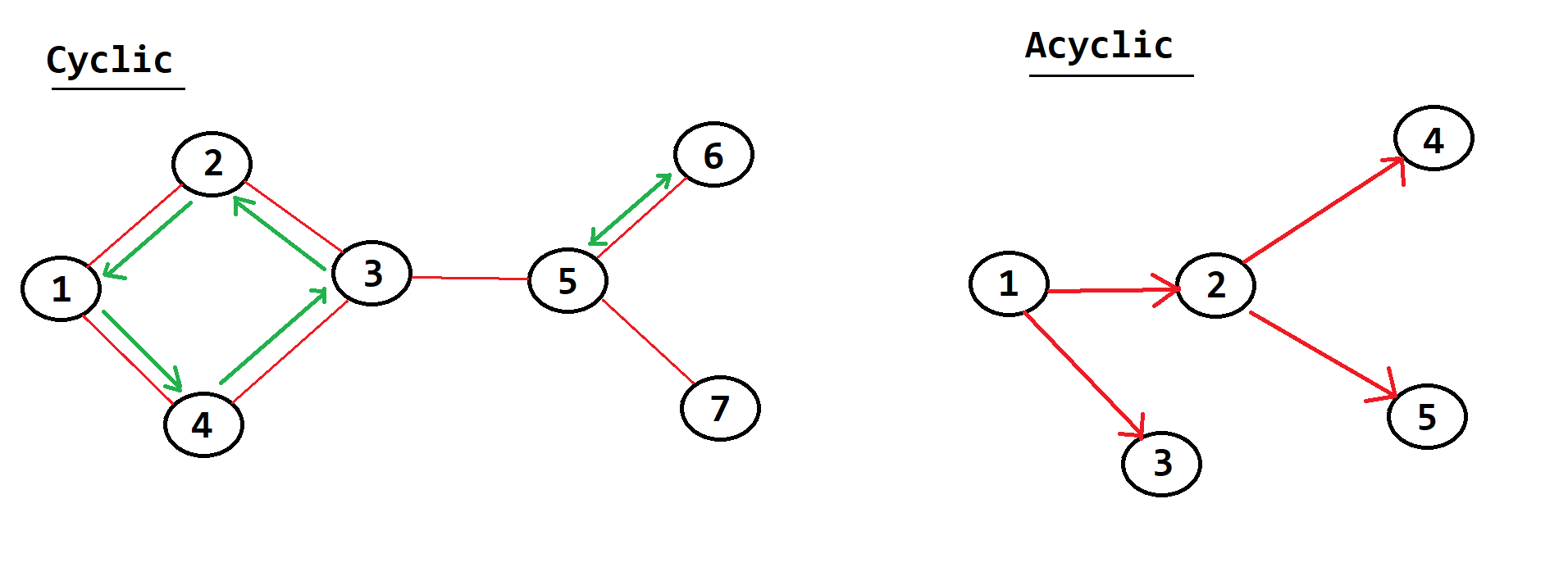
Cyclic & Acyclic

Cyclic

  • Contains a path from at least one node back to itself, example node 4 leads to 3, which leads to 2, which leads to 1 and finally back to 4 (this is a small cycle)
  • All Undirected graphs end up being cyclical, this is because the bi-directional natute of the nodes within undirected graphs theoretically forms a cycle between any two nodes

Acyclic

  • Contains no path from any one node which leads back in on itself
  • This property can only really be applied to Undirected Graphs

graph: properties cyclic and acyclic

Weighted

  • This applies to the edges of the graphs instead of the nodes
  • Associating a numerical value with each edge (aka cost)
  • Each weight represents some property of the information you’re trying to convey

graph: weighted

6 Types

Combining graph properties can create the following types of graphs, additionally any of them can have the weight property. So there are 6 differenty types of graphs.

  • Cyclic Undirected
  • Cyclical Directed
  • Acyclical Directed
  • Cyclic Undirected with weighted Edges
  • Cyclical Directed with weighted Edges
  • Acyclical Directed with weighted Edges

  • Undirected Cyclical Heaps with weighted Edges

    • Dijkstra’s shortest path algorithm
    • Compiles a list of the shortets possible paths from that source vertex to all other nodes within the graph
    • Google use this algorithm with its maps, its used in the process of IP routing and can be used in telephone networks

  • Un-weighted Cyclical Graphs (Undirected and Directed)

    • Are used in the follower system of a majority of social media websites like Facebook, Instagram, Twitter ect

Traversals

Graph Traversals: Depth First Search (DFS), Breadth-first search (BFS)

References

Heaps

Use case:

  • Commonly used in the implementation of
    • HeapSort, a sorting alorithm which takes in a list of elements, builds them into a min/max heap, and then removes the root node continuously to make a sorted list
    • priority queues which is an advanced data structure which your computer uses to designate tasks and assign computer power based on how urgent the matter is

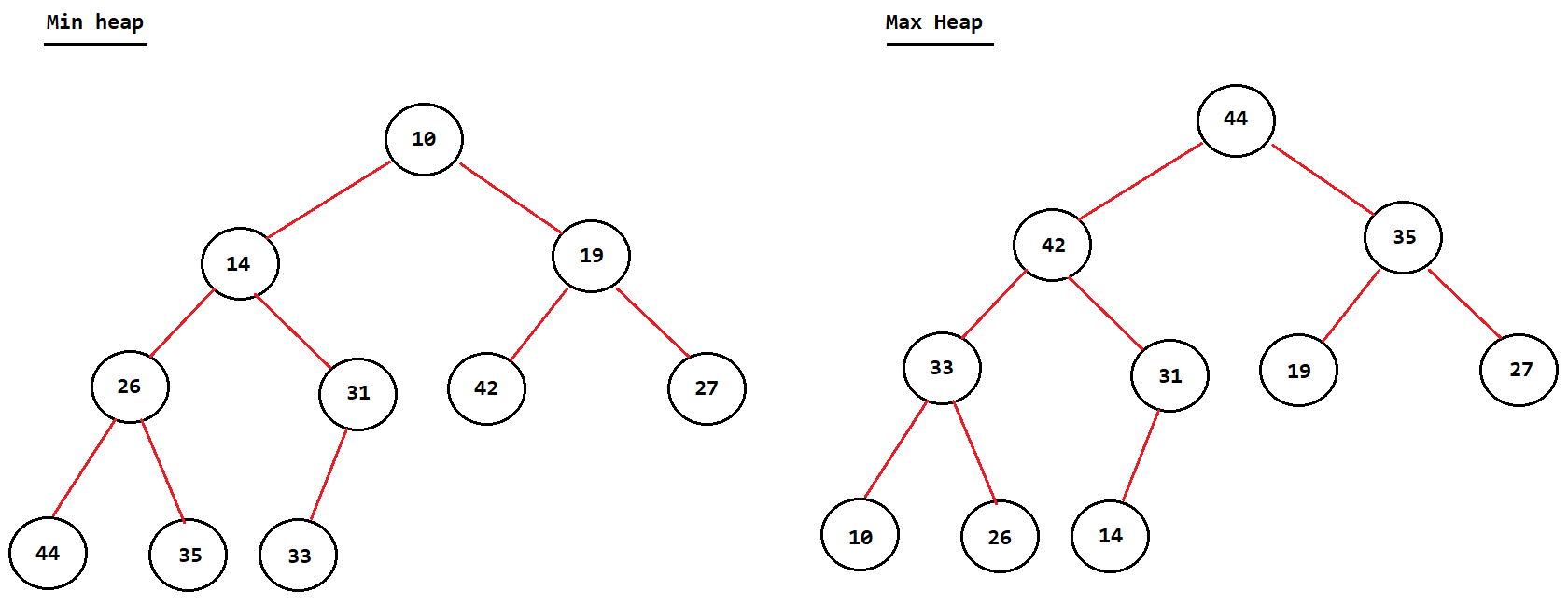
heaps

  • Each node can only have 2 children
  • A special tree where all parent nodes compare to their children nodes in some specific way
    • Determines where the data is stored
    • Usually dependent on the parents node value
  • Min heap
    • The value at the root node of the tree must be the minimum amongst all of its children
    • This fact must be the same recursively for all the parent nodes contained within the heap
  • Max heap
    • The value at the root node of the tree must be the maximum amongst all of its children
    • This fact must be the same recursively for all the parent nodes contained within the heap
  • Basically like binary trees and usually min/max heaps that have a special property.
  • Helpful when you need to repeatedly find the smallest and largest values in groups of values.

Adding to the heap

  • When building the heap we always start at the left, if the left child is taken then we add to the right.
  • Finally recursively swap nodes based on the heap type min or max

Deleting from the heap (root node)

  • Remove root node from the heap (Well its value)
  • Replace it with the node furthest to the right
  • heapify the heap by comparing the parent nodes to their children and swapping if nexessary

References

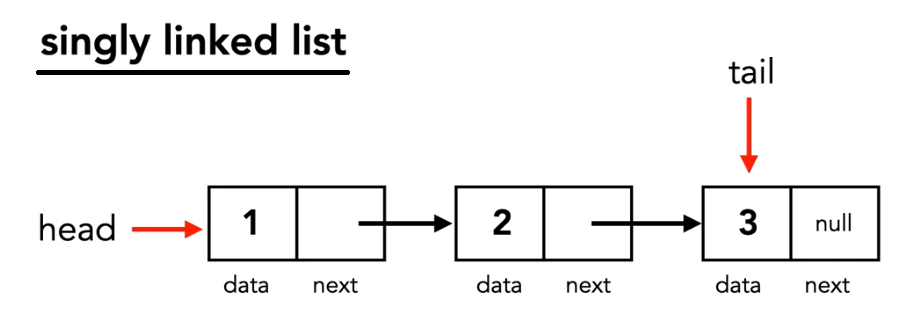
Linked List

Use case: could be to implement other data structures like stacks, queues and hash tables. Operations would be search, insert and delete

Data structure for storing objects in linear order, each object has data and a pointer to the next object. Simliar to arrays except pointers determine ordering not the array indices.

singly linked list (pointers are in one direction)

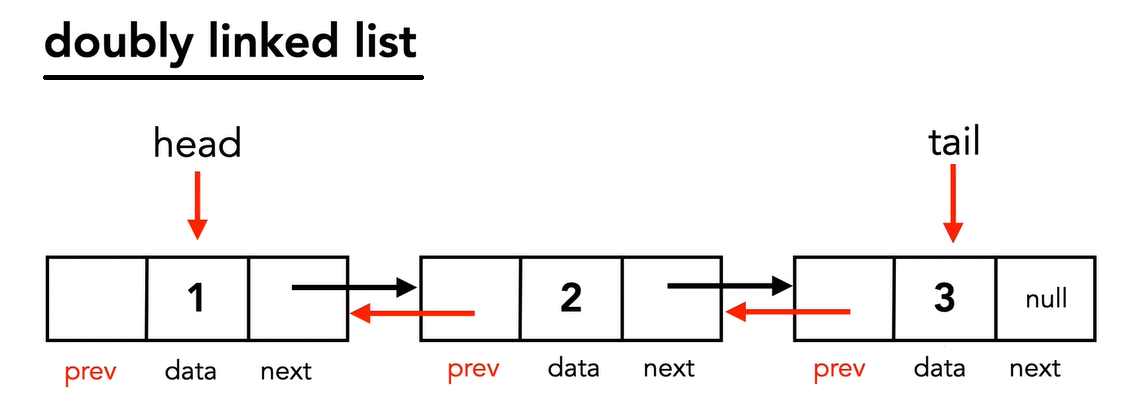
Additionally there are doubly linked lists.

doubly linked list (prev pointer points to the object infront of it in the chain)

And circular linked lists.

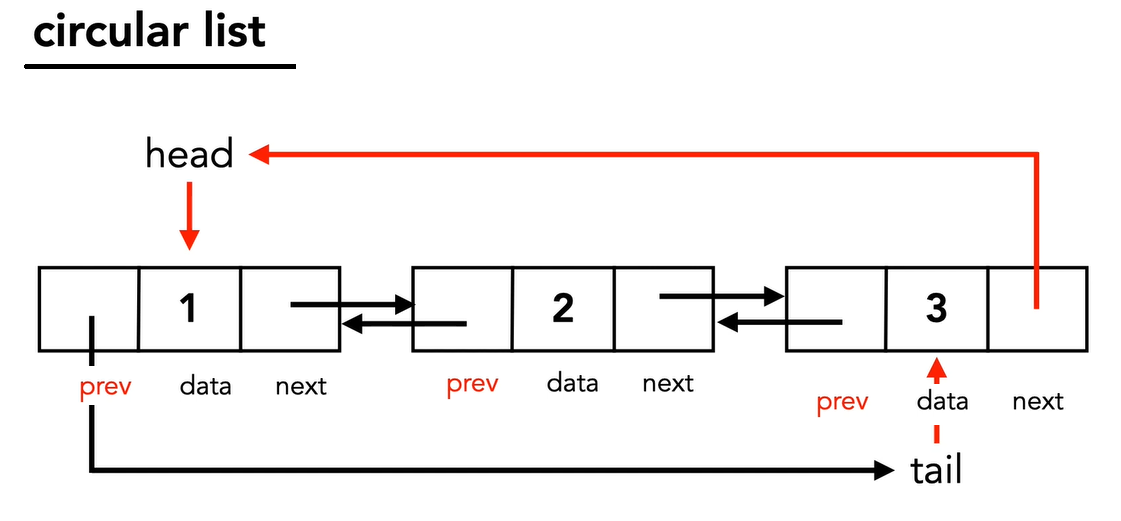
circular linked list (prev pointer of head object points to the tail, the next pointer of the tail object points to the head)

References

Queues

Complexity:

  • O(n) for accessing/searching (this is because you have to go though each element to get the one you want, complexity defaults to worst case)
  • O(1) for inserting/deleting as its always at either the head or tail

Use case: Job scheduling, printer queue, modern cameras (Google pixel phones) would use them for zero shutter lag (the time between when you take a picture and what the phone actually captures)

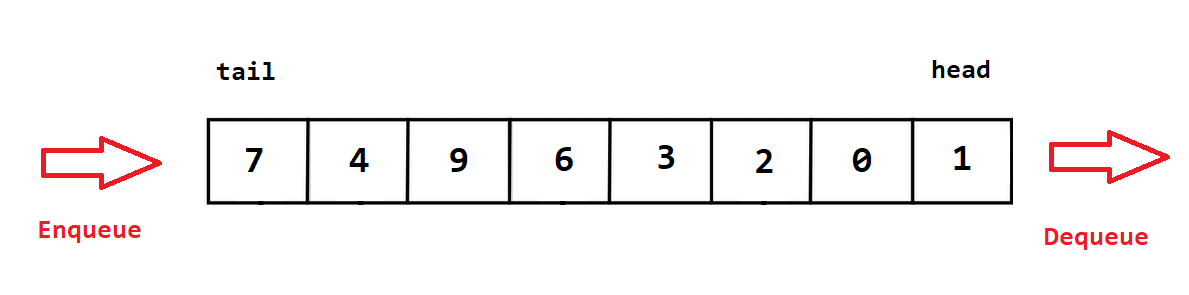
queue (FIFO)

A queue is a sequential access data structure that follows the FIFO methodology (First-In, First-Out), this means we can only access the elements contained within it in a certain way.

The first element added to the queue will always be the first one to be removed. New elements are added to the tail (aka rear or back) and are removed from the head (aka front) until all elements are removed.

Elements are added with Enqueue(object) and removed with Dequeue(). Additionally to can Peek() to check whats at the head without removing it or run Contains(object) to check if an element value matches what you are looking for.

1
2
3
4
5
6
7
8
using System.Collections;
var myQueue = new Queue();

myQueue.Enqueue("foo");
myQueue.Enqueue(42);

myQueue.Peek      // get the head element in the queue without removing it
myQueue.Dequeue   // get and remove the head element

References

Stacks

Complexity:

  • O(n) for accessing/searching (this is because we have to pop off elements to get to the one we are looking for, complexity defaults to worst case)
  • O(1) for inserting/deleting as its always at the head

Use case: Recusion uses stacks as a way of keeping of active functions/sub-routines. Undo/Redo in a word processor, back paging on web engines.

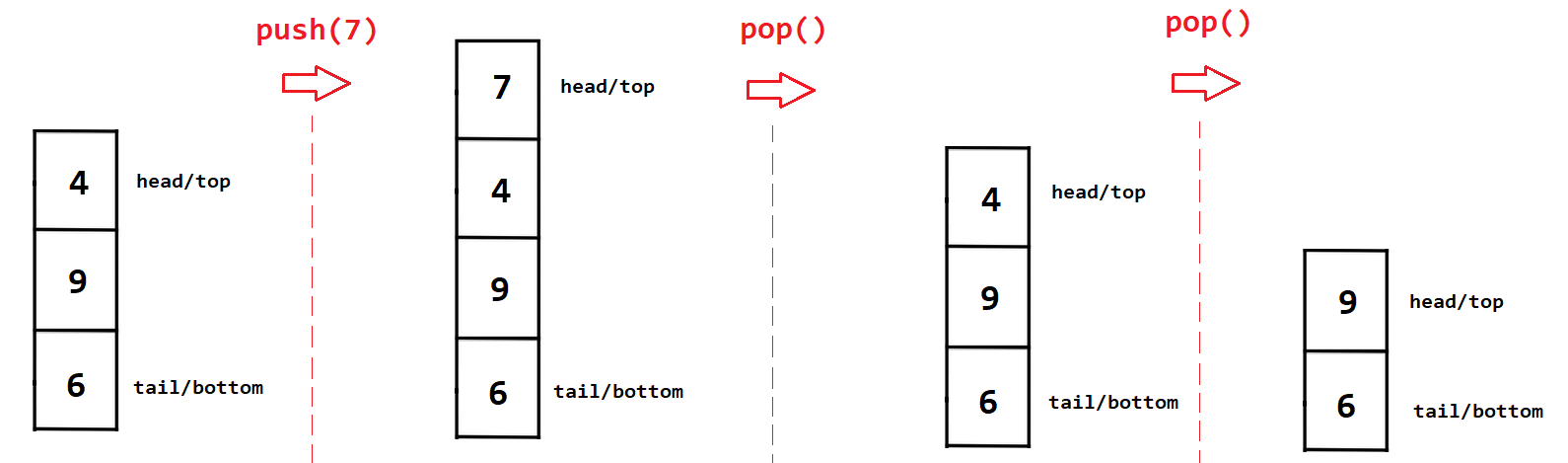
stack (LIFO)

This is a sequential access data structure, the elements can only be accessed in a particular order. Each element is dependat on the others and may only be obtained though those other elements. Elements are added using LIFO methodology (Last-In, First-Out)

Last element pushed onto the stack would be the first one popped off, this means there is only one way in and out for the data.

Elements are added with Push(object) and removed with Pop(). Additionally to can Peek() to check whats at the head without removing it or run Contains(object) to check if an element value matches what you are looking for.

1
2
3
4
5
6
7
using System.Collections;
var myStack = new Stack();

myStack.Push(7);

myStack.Peek      // get the head element in the queue without removing it
myStack.Dequeue   // get and remove the head element

References

Trees

Use case: Storing data in a hierarchically structure. File structure, Family tree, Company corporate structure.

Trees store data hierarchically as opposed to lineraly like a list. They have a specific starting point (the root node) with two branches however they can also have one or no branches.

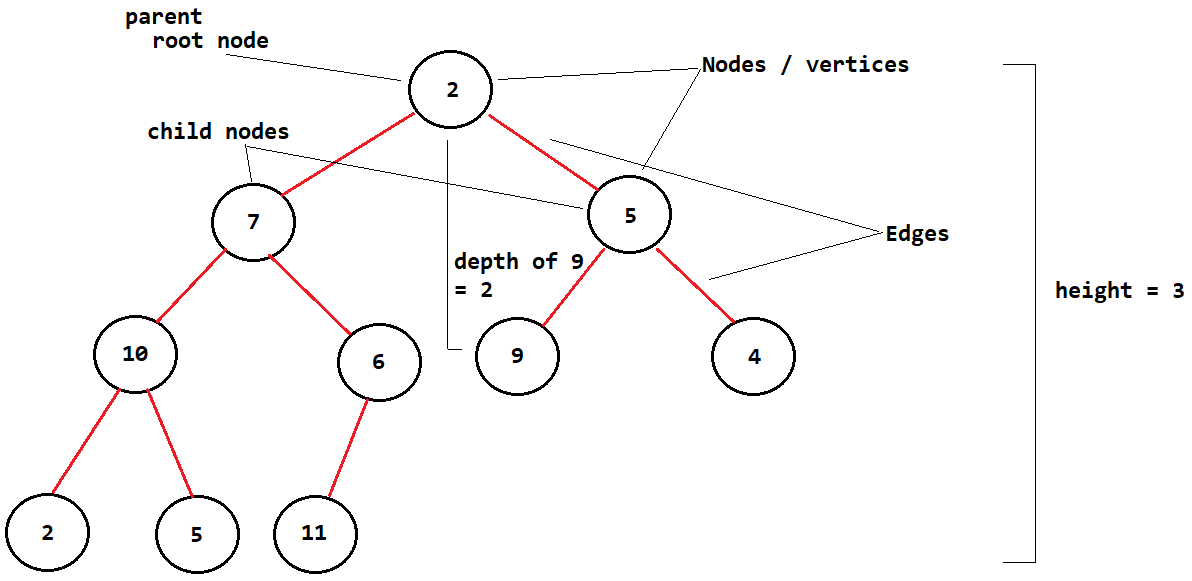
trees

  • Trees are an abstract data structure which contains a series of linked nodes connected together to form a hierarchical representation of information
  • The topmost node of a tree is the root node, connected to it (if anyt) are child nodes
  • A parent node has 1 or 2 child nodes
  • Each node in a tree are called vertices
  • Connections between vertices are called edges
    • There is only one path between any two vertices, you cannot have more than one edge connectiong two vertices
  • leaf nodes have no children

Tree Properties

  • Height is the number of edges on the longest possible path down towards a leaf
  • Depth is the number of edges required to get from that node to the root node

Types of trees

By imposing rules and restrictions on what type of data is stored within a tree and also where we can use a tree structure to its full potential

There are many types, these are just a few

  • AVL Tree
  • Binary search tree
  • Suffix Trees
  • Re-Black Tree
  • N-ary Tree

References

General References