Invert A Binary Tree (BST)

Poking some fun

This is a Rosetta Code post.

Story

Another popular interview question/assessment is to invert a binary tree. This is where all the left and right children of all non-leaf nodes are interchanged. Think of it as a mirror of the input tree.

This can be visually understood as follows, where 4 is the root node and its subsequent children are inverted.

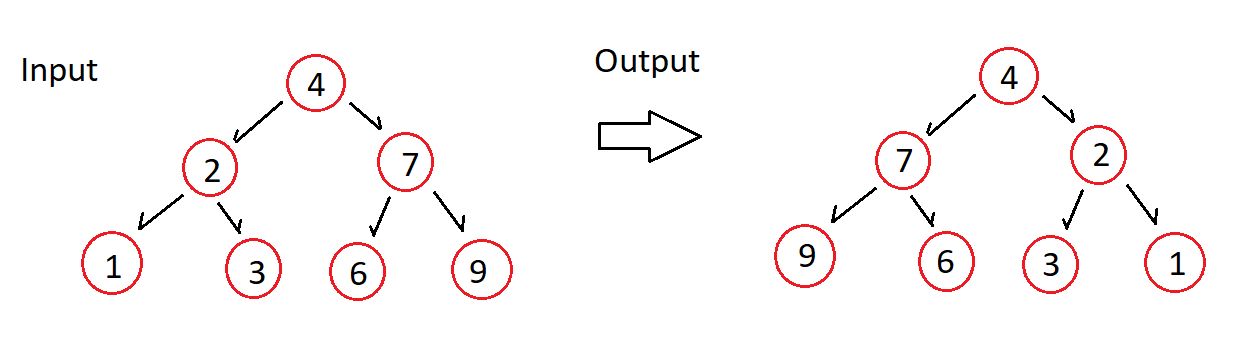
Invert Binary Tree Example

What exactly is a binary tree?

Its simply a data structure

  • Used to represent data in a hierarchical format starting from the root node, the subsequent nodes are left/right children nodes
  • Every node has 2 components, Data (so its value) and references. These references are either null or a reference to the left/right children
  • Adding data to a tree starts at the root node, if its not null the value is added at the root. If the value to be added is LESS than the root its added on the LEFT. If its greater its added on the right. This pattern builds the entire tree and is then performant for searching.

Task 1

Given the binary tree from the story above, invert it so its values show as the example Output. Its important to remember that its a mirror image so the left and right children are swapped. (Dont try flip it so the root node is at the bottom)

Solutions

Some of the code below is based on the hilarious Inverting Binary Trees - You Suck at Coding [1] video by Ben Awad. The rest is base on learnings from Data Structures and Algorithms in C#

This would be my pseudocode, I feel its important to try set yourself up for success - pseudocode is part of the journey.

  1. Understand what the class will look like
1
2
3
4
5
class BstNode {
  int data;
  BstNode left;
  BstNode right;
}
  1. There are many ways to do this (see the references at the end) but upfront we need to atleast choose one of
  • Iterative - this is when a loop repeatedly executes until the controlling condition becomes false.
  • Recursive - this is when a statement in a function calls itself repeatedly.

Recursion is how most of the online examples are doing it so lets roll with that.

  1. Ensure you have a base case
1
2
3
if (left == null && right == null) {
    return;
}
  1. In the function swap the nodes
1
2
3
var temp = node.left;
node.left = node.right;
node.right = temp;
  1. Call the inversion function with each node
1
2
Invert(node.left);
Invert(node.right);

Task 2

Given the following binary tree, invert it from the specified node.

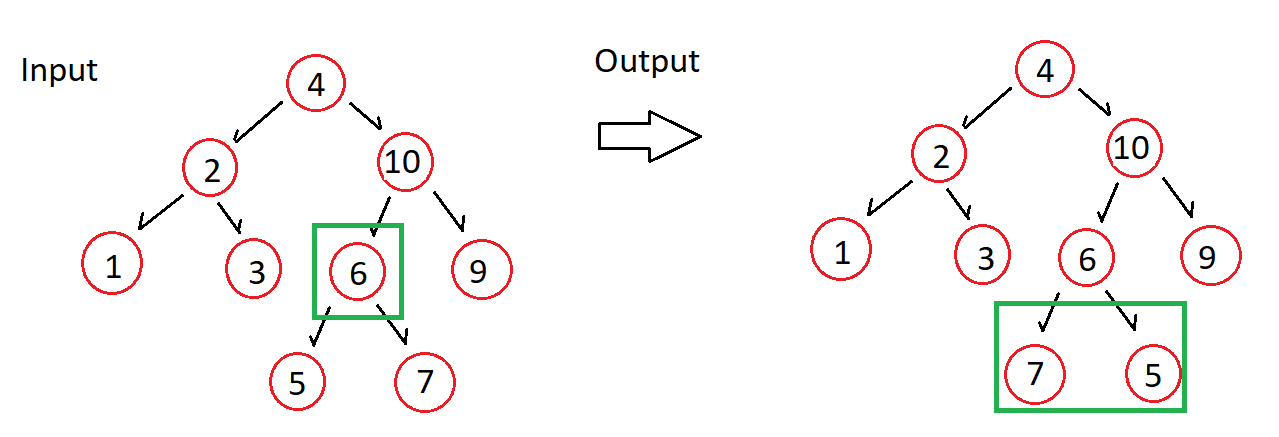
Task 2: Invert from specified node

Solutions

pseudocode

  • Use recursion to find the node we are interested in inverting from
  • Use recursion to invert from there the same as we did in task 1 above

Example code to traverse recursively

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class BstNode {
  int data;
  BstNode left;
  BstNode right;
}

public void Traverse() {
  if (left != null) {
    left.Traverse();
  }
  Console.WriteLine(this.data);
  if (right != null) {
    right.Traverse();
  }
}

References