Big O Notation

“In computer science Big O notation is useful in the analysis of algorithms” - wikipedia.org

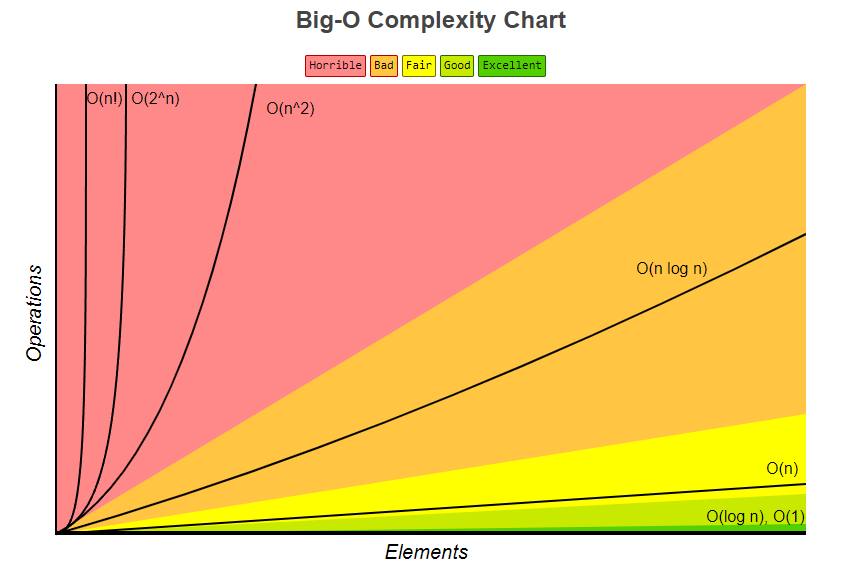
This illustation is from https://www.bigocheatsheet.com/ and is the most popular I’ve seen online.

www.bigocheatsheet.com

1
2
3
4
5
6
7
O(1)         Constant                  Looking up by index, no matter the array size it will always take the same amount of time
O(log n)     Logarithmic               Needs a sorted array, halving the data each time like a binary search
O(n)         Linear                    1 to 1 relationship of inputs "n" and the amount of time needed to executed
O(n log n)   Log linear complexity
O(n^2)       Quadratic                 inputs raised to the power of 2 (a loop within a loop) ~ could also be called N squared
O(2^n)       Exponential               looping over every possible combination in an array
O(n!)        Factorial

Definition

  • Simplified analysis of an alorithms efficiency / time complexity.

One of my peers once explained this to me as being able to use this in regards to problem solving.

Example: what’s the big O of xs.map(...).filter(...).find(...)

What Is Big O?

  • Complexity in terms of the input size, n. How well will the algorithm perform as its input size grows.
  • Abstract the efficiency of our algorithms or code from the machine (its independent)
  • Examine the basic computer steps of the code
  • Can analyze both time complexity (how long it takes to run) and space complexity (how much memory it needs)

Types of measurement

Typically look at worst case but we have to be cognizant of best and average case, its dependant on the application/algorithm

  • Worst case (typically used)
  • Best case
  • Average case

General rules

  • Ignore constants for trivial examples, example a running time of 5n, it runs on the order of O(n). This is because as n gets large the 5 no longer matters
    • in practice constants matter, a constant of 2 or 3 could have a large impact
  • The same way as n grows certain terms dominate others.
    • Example O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^n) < O(n!)
    • this means we ignore/drop lower order terms when dominated

O(1) Constant time / complexity

Complexity: Excellent

Independent of input size n it takes a constant time to complete. Like 14 nanoseconds, or three minutes no matter the amount of data in the set.

1
x = 5 + (15 * 20);         ~ O(1) big O of 1

Sequence of statements in constant time

1
2
3
4
5
6
x = 5 + (15 * 20);         ~ O(1)
y = 15 = 2;                ~ O(1)
print x + y;               ~ O(1)

this is 3 * O(1)
as we drop constants its just O(1)

O(log n) Logarithmic time / complexity

Complexity: Good

“The best way to wrap your head around this is to remember the concept of halving: every time n increases by an amount k, the time or space increases by k/2.”

An example of this is binary search, see Invert A Binary Tree (BST).

O(n) Linear time / complexity

Complexity: Fair

Increases linearly and in direct proportion to the number of inputs.

1
2
3
4
for x in range (O, n):
   print x;               ~ O(1)

the block of code is n * O(1) which is the same as O(n)
1
2
3
4
5
6
7
y = 5 + (15 * 20);        ~ O(1)
for x in range (O, n):
   print x;               ~ complete for loop is O(n)

total time is the summation of these two = O(1) + O(n)
we drop low order terms when n gets large, the time to compute y is meaningless
the result is then O(n) this is because the for loop dominates the run time

O(n log n) loglinear complexity

Complexity: Bad

O(n log n) grows logarithmically, which means that the time it takes to run the algorithm will increase slowly as the input size increases.

“O(n log n) implies that log n operations will occur n times.”

O(n^2) quadratic time / exponential time

Complexity: Horrible

O(n^2) grows quadratically, which means that the time it takes to run the algorithm will increase much more quickly as the input size increases.

It takes n*n operations, example is a nested loop.

With Big O we usually look at worst case scenario, for the examples below the largest runtimes are O(n^2)

1
2
3
4
5
6
7
8
9
x = 5 + (15 * 20);         ~ O(1)
for x in range(0, n):
   print x;                ~ complete for loop if O(n)
for x in range(O, n):
   for y in range(O, n):
      print x * y;         ~ complete for the nested loops is O(n^2)

this is executed at n * n which is O(n^2)
the nested for loop dominates here, the result is O(n^2)

Additionally we can have O(nˣ) or polynomial complexity which is just a range of possible values that x could be, generally for ccomputer science we are talking about x being 2.

O(2^n)

Complexity: Horrible

O(n!) factorial

Complexity: Horrible

“O(n!), or factorial complexity, is the “worst” standard complexity that exists. To illustrate how fast factorial solutions will blow up in size, a standard deck of cards has 52 cards, with 52! possible orderings of cards after shuffling.”

Additional Concepts

When I was researching Big O notation these concepts came up a lot specifically in content from Clément Mihailescu Co-Founder of https://www.algoexpert.io/

Sliding Window Technique

Involves manipulating two pointers or two indices at the same time as you’re traversing thought something like a string or an array. Basically you have a left pointer/index and a right pointer/index and your move them simultaneously in an array or a string. (could be to count frequency of characters)

Recursion

A lot of problems can be solved easily with recursion (as apposed to iteratively). This produces cleaner and less code than an iterative approach. Example problems that help you understand recursion include:

  • n fibonacci
  • calculate height of binary tree or the depths of nodes in a binary tree

Dynamic Programming (DP)

It means being able to solve a problem that is complex by first solving a smaller version of that problem. To solve that small version of the problem you solve an even smaller version of that problem, until you can solve a trivial version of the problem. The only way to get good at DP is to do a lot of DP!

References